Using the method used by Thales to find the height of the Cheops pyramid eons ago, you can find the height of anything that the sun casts a shadow of.  Oddly, it seems that few people I know know this trick. I'm pretty sure I learned it in 6th grade geometry, maybe I taught it to my self, I did learn most of what I know about mathematics and physics on my own. But this does seem to have been forgotten or otherwise unknown to many.

This method is quite simple as long as you understand very basic Algebra and minimal Trigonometry.  It was also referenced in the Sherlock Holmes story The Musgrave Ritual to find the height of an oak tree to help solve the riddle.

So, I'll demonstrate.  For some reason, I wanted to know the height of the flagpole in our front yard.  I will use a plant hanger as a reference.

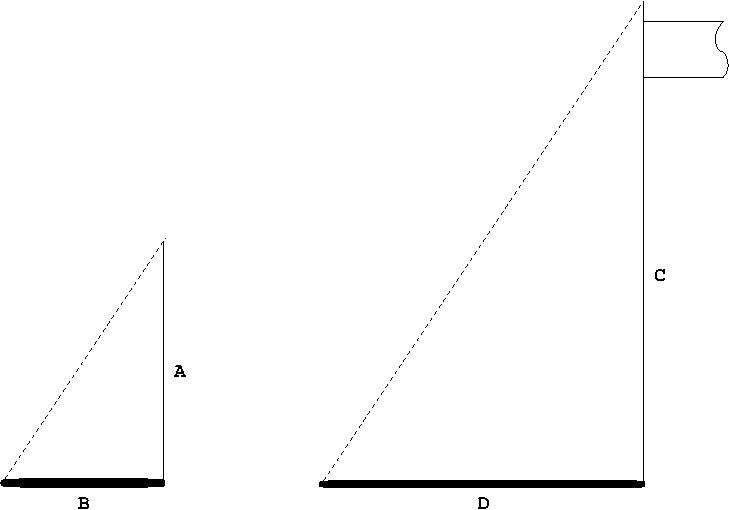
A is the Height of the plant hanger, B is the length of it's shadow.  D is the length of the flag poles shadow, and C, the height of the Flag pole is what we are looking for.

Compliments of the AAA similarity theorem, we know that:

$$\frac{A}{C} = \frac{B}{D}$$

So I used a tape measure to get A = 6ft 5in , B = 8ft 9in , and D = 20ft 5in.

After converting to inches:

$$\frac{77in}{C} = \frac{105in}{245in}$$

And we solve for C:

$$C = \frac{77in * 245in}{105in} = 180in$$

And we find that the flag pole is 180 in, or 15 feet high.