Some times it’s necessary to calculate a series, be it a summation or integral that has infinity as one it’s boundaries.  Well, most modern scientific calculators aren’t really Computer Algebra Systems and therefor don’t understand what infinity is. But, depending on the accuracy needed, and how fast it converges, normally using 100 or 1000 is good enough. Sometimes, it does take a little bit of tweaking.  But, in general, it’s not hard to work out.

NOTE: All the examples are done on a Casio Prizm, but the principle is the same, and it should apply to any calculator that can do summations and integration.

NOTE: I’m going to assume you know how to use your calculator to do summations and integration problems.

As an example, here is a summation that is known to converge on 1:

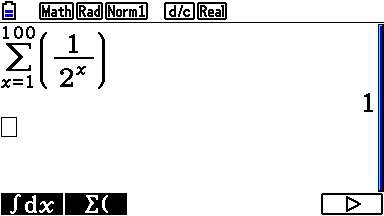
In this case, 100 was good enough to replace infinity with.

Here is another example from the era of Newton:

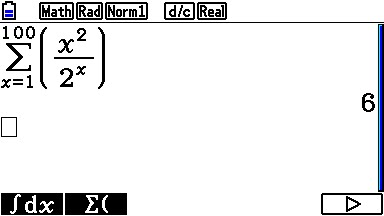
Sometimes, to get more accuracy, you may need to add a zero or two:

This one converges on ln 2, and using 1000 gets close enough for most applications, but if you need more accuracy, you may need to go to 10000 or even higher.

The Same principle applies to integrals:

Just as before, sometimes you have to add 0’s to get the accuracy you may want:

This one converges on pi/2, but it could take adding a few zeros.

Sometimes, to get to the real answer, you need to play with it a bit:

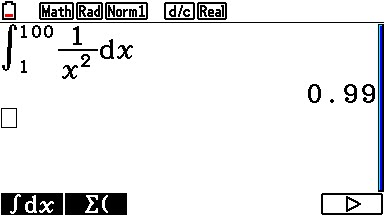
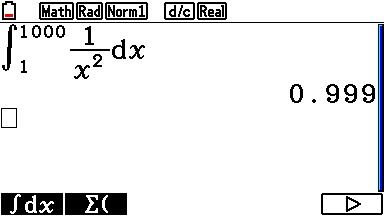
In these two examples, you can see that as you add zeros, you and 9’s to the accuracy.  Since 0.99999... = 1, this series converges on 1 ( which it does ).

As you can see, it’s not hard to simulate infinity, with in the accuracy confines of your calculator.  Just remember, the more zero’s you add, the longer it will take to calculate.  In the above examples, none of them took more than a few seconds, most came back instantly. But on an older or slower calculator, it may take time to process.